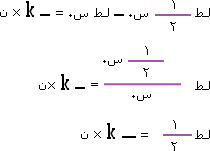الحركية الكيميائية

فإذا كانت س =

س₀ أي إذا استهلكت نصف الكمية المتفاعلة وبقي نصفها فإن :

لـط₁ ـ لـط₂ = ـ k × ن

صفر ـ لـط₂ = ـ k ن

لـط₂=

ن ................... بضرب طرفي المعادلة في (-1) .

ومنه

و ن هو الزمن اللازم لتفاعل نصف الكمية ومن الواضح أن ن = مقداراً ثابتاً لأن k هي ثابت التفاعل ، لـط₂ = قيمة ثابتة = 0.693 ( وهذه القيمة مقربة لثلاث منازل عشرية ).

إذن زمن نصف العمر لتفاعل من الدرجة ( الرتبة ) الأولى = مقداراً ثابتاً هو

ولا يعتمد ولا يتأثر بتراكيز المواد المتفاعلة ويبقى دون تغيير

طيلة فترة تحول المواد المتفاعلة إلى المواد الناتجة .

وحتى نميز زمن نصف العمر عن أي زمن آخر يمكن أن نرمز له بالرمز

أو أي رمز آخر .

وبناءً على ما سبق يمكن أن نجد زمن الوصول للتركيز المتبقي من العلاقة ....... (1) ، بافتراض أن التركيز الابتدائي = 1 فيكون لـط س0 = لـط(1) = صفر .

إذن لـط س ( التركيز المتبقي بالنسبة للتركيز الأصلي ) = ـ k × ن .

أما لـط س فإنه يساوي 2.3 لو س .

العلاقة بين لـو العدد و لــط العدد هي لـط العدد = لـو العدد × 2.3 وذلك بالتقريب لمنزلة عشرية واحدة .

1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |12 | 13 | 14

اعداد : أ . سليم حمام	اكتبوا لنا ملاحظاتكم واستفساراتكم
تاريخ التحديث :تموز 2008	تحرير : المدرسة العربية www.schoolarabia.net