|
||||||||||||||||||
3- اتفاق واختلاف مجموع ريمان مع المساحة المحصورة بين منحنى الاقتران ومحور السينات.
سندرس فيما يلي علاقة مجموع ريمان بالمساحة المحصورة بين منحنى الاقتران ومحمور السينات من خلال مجموعة تالبة من الأمثلة على اقترانات متزايدة واقترانات متناقصة، وأيضاً كيف تتأثر هذه العلاقة بعدد فترات التجزئة.
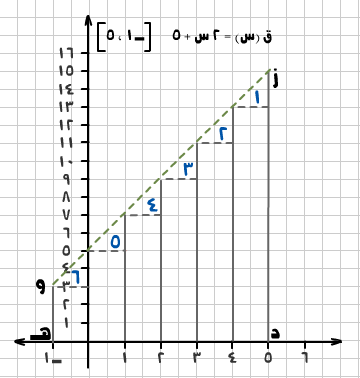
مثال (1): أوجد مجموع ريمان للاقتران ق(س)= 2 س + 5 في الفترة [ -1 ، 5 ] على أن يكون عدد الفترات 6.
الحل: - ما نوع الاقتران ق (س) = 2 س + 5 أمتزايد أم متناقص؟ اختر الإجابة الصحيحة. - عدد فترات التجزئة 6 .
|
||||||||||||||||||
|
Copyright © 2001 - 2012 SchoolArabia. All rights reserved الحقوق القانونية و حقوق الملكية الفكرية محفوظة للمدرسة العربية |
||||||||||||||||||