مجموع ريمان

[ 0 ، 3 ] فالمطلوب إيجاد المساحة المحصورة بين

مثال (2): إذا كان ق (س) = س² + 1 حيث س

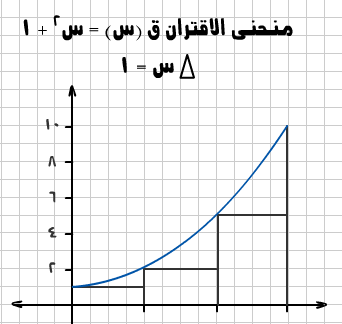
منحنى هذا الاقتران (في الفترة المعطاة) ومحور السينات باستخدام مجموع ريمان وبتجزئة ثلاثية للفترة.

الحل:

نكون جدول نحدد فيه النقاط اليسارية واليمينية من الفترات باعتبار

س*ر = س _{ر – 1} أي نأخذ النقاط اليسارية للفترات نملأ الجدول ونرسم فنجد أن مساحة المستطيلات = وحدات مربعة، وهي أقل من المساحة المطلوبة (لاحظ الشكل (1)).

ل × ق(س^*_ر)	ق(س^*_ر)	س^*_ر = س _ر-1	ل طول الفترة الجزئية	الفترات الجزئية [ س_{ر ـ 1} ، س_ر ]
1	1	0	1	0 ، 1
2	2	1	1	1 ، 2
5	5	2	1	2 ، 3
8

شكل (1): توصيل النقاط اليسارية للتجزئة الثلاثية.

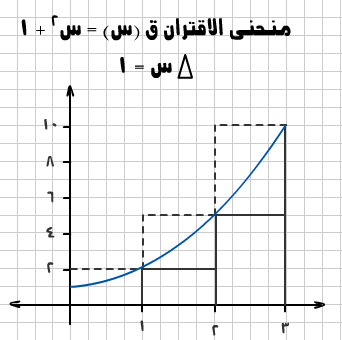
وفي حال أخذ النقاط اليمينية نحصل على الجدول التالي:

ل × ق(س^*_ر)	ق(س^*_ر)	س^*_ر = س _ر	ل طول الفترة الجزئية	الفترات الجزئية [ س_{ر ـ1} ، س_ر ]
2	2	1	1	0 ، 1
5	5	2	1	1 ، 2
10	10	3	1	2 ، 3
17

ويلاحظ من الشكل (2) أن مساحة المستطيلات أكبر من المساحة المطلوبة.

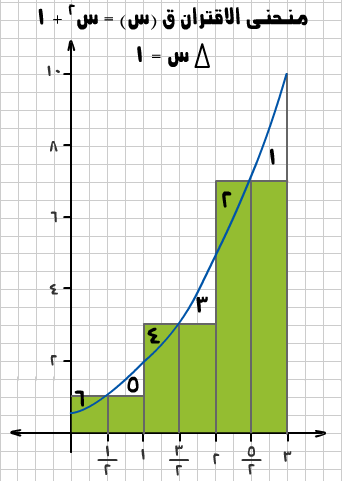
شكل (2): توصيل النقاط اليمينية للتجزئة الثلاثية.

ولو أخذنا معدل المساحتين السابقتين نجد أن:

وحدة مربعة وهي أقرب إلى واقع المساحة المطلوبة.

ولو وصلنا نقاط منتصف الفترات لحصلنا على الجدول التالي (لاحظ الشكل (3) أيضاً).

ل × ق(س^*_ر)	ق(س^*_ر)	س^*_ر = س _ر	ل طول الفترة الجزئية	الفترات الجزئية [ س_{ر ـ 1} ، س_ر ]
			1	0 ، 1
			1	1 ، 2
			1	2 ، 3

شكل (3): توصيل نقاط منتصفات الفترات للتجزئة الثلاثية.

وحدة مربعة قريبة من المساحة الحقيقية والتي هي بالضبط = 12 وحدة مربعة.

لاحظ أن المساحة

اكتبوا لنا ملاحظاتكم واستفساراتكم
تحرير: المدرسة العربية www.schoolarabia.net	إعداد: أ. فائق الفّرا / أ. سليم حمام
	تاريخ التحديث: آب 2002
	تاريخ التحديث: تموز 2012