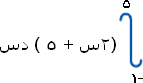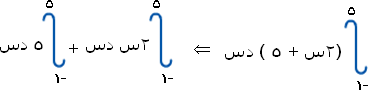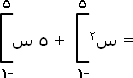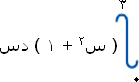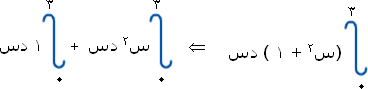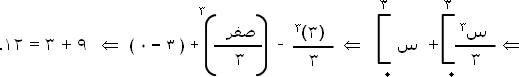مجموع ريمان

مثال (3):

			الحل:

(5)² – ( -1 )² + ( 5 × 5 ) – ( 5 × -1 )

( 25 – 1 ) + ( 25 + 5 ) 24 + 30 = 54

ارجع إلى مثال (1) لقد حسبنا فيه المساحة المحصورة بين منحنى الاقتران ق (س) = 2 س + 5 (وهو نفس مثال 3) ومحور السينات ووجدنا أنها 54 وحدة مربعى وفي مثالنا هذا (3) وجدنا التكامل المحدود للاقتران نفسه فحصلنا على نفس الرقم (54)، إي يمكن إيجاد المساحة إما بطريقة ريمان (مجموع ريمان) أو بالتكامل المحدود.

مثال (4):

	الحل:

فإذا عدنا إلى مثال (2) الذي حسبنا فيه المساحة المحصورة بين منحنى الاقتران ق (س) = س² + 1 (وهو نفس مثالنا 4 هنا) نجد أن المساحة المحصورة كما حسبناها بمجموع ريمان كانت قريبة من هذا الرقم ( 12 ) حيث كانت تساوي ( 11.75 ) حينما أخذنا نقاط منتصف الفترة.

يتضح من المثالين 3 ، 4 أن المساحة المحصورة بين منحنى اقتران ما ومحور السينات خلال فترة محددة يمكن الحصول عليها إما بطريقة مجموع ريمان أو بطريقة التكامل المحدود.

اكتبوا لنا ملاحظاتكم واستفساراتكم
تحرير: المدرسة العربية www.schoolarabia.net	إعداد: أ. فائق الفّرا / أ. سليم حمام
	تاريخ التحديث: آب 2002
	تاريخ التحديث: تموز 2012