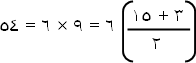ج) المطلوب حساب م ( 3 s ، ق ) حيث كما ذكرنا في أ ، ب (3 s ) تجزئة ثلاثية منتظمة، ولكننا سنحسب قيمة الاقتران عند منتصف كل فترة من الفترات الثلاث.

ق (صفر) = 2 (صفر) + 5 = 5.

ق (2) = 2 (2) + 5 = 9.

الفترة الجزئية الثالثة: [ 3 ، 5 ] ومنتصفها عند  س = 4.

ق (4) = 2 (4) + 5 = 13.

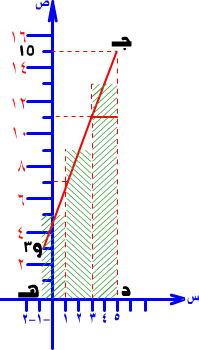
انظر الشكل (3): مجموع مساحة المستطيلات الناجمة عن توصيل نقاط منتصف الفترات الجزئية الثلاث = ( 2 × 5 ) + ( 2 × 9 ) + ( 2 × 13 ) = 10 + 18 + 26 = 54 وحدة مساحة.

شكل (3)

وهي تساوي بالضبط قيمة المساحة المحصورة بين منحنى الاقتران ومحور السينات.   والآن لنعد إلى ( أ ) حيث أخذنا المساحة الناتجة عن توصيل النقاط اليسارية للفترات فكانت 42 وحدة مساحة وهي أصغر من المساحة الحقيقية.   وعندما أخذنا في ( ب ) المساحة الناتجة عن توصيل النقاط اليمينية للفترات كان الناتج 66 وحدة مساحة وهي أكبر من المساحة الحقيقية.   لوجدنا أنها تساوي 54 ولو أخذنا الآن متوسط المساحتين وحدة مساحة والتي هي المساحة الحقيقية والتي تساوي مساحة المستطيلات الناتجة عن توصيل نقاط أنصاف الفترات الثلاث.

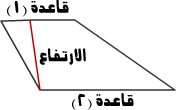
لاحظ أيضاً أن المساحة الحقيقية المطلوبة هي مساحة شبه المنحرف جـ د هـ و التي تساوي

ملحوظة (1): لقد اعتمدنا في الفروع أ ، ب ، جـ على أن التجزئة منتظمة (أي أن أطوال الفترات الجزئية متساوية).

ملحوظة (2): النقطة التي نريد إيجاد قيمة الاقتران عندها نرمز لها بالرمز س*ر .