مجموع ريمان

شكل (3)

- أعد رسم منحنى الاقتران وصل بين نقاط منتصفات الفترات ولاحظ مجموع مساحات المستطيلات الناتجة (انظر الشكل (3))، احسبها واجمع مساحاتها تجد أنها 48 وحدة مربعة أي أنها تساوي المساحة المطلوبة.

لاحظ المثلثات الملونة بالأزرق والتي حسبت مساحتها مع المساحة المطلوبة مع أنها خارجها تعادل مساحات المثلثات الملونة بالأخضر التي لم تحسب مع المساحة المطلوبة مع أنها واقعة ضمنها، وبعبارة مختصرة:

مجموع مساحات المثلثات التي أضيفت للمساحة المطلوبة تساوي مجموع مساحات المثلثات التي طرحت منها.

أعِد دراسة مثال (2) دراسة دقيقة ودقق أيضاً في الأشكال التوضيحية

1 ، 2 ، 3، ثم اختر الإجابة الصحيحة لكل سؤال مما يلي:

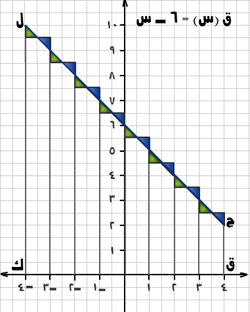
- الاقتران المدروس ق (س) = 6 – س هو اقتران: متزايد أم متناقص.

- المساحة الناتجة عن توصيل نقاط التجزئة اليسارية (أصغر أم أكبر) من المساحة المطلوبة.

- المساحة الأقرب إلى المساحة الحقيقية هي مساحة المستطيلات الناتجة عن توصيل نقاط التجزئة (اليمينية أم اليسارية أم لمنتصف الفترات).

- كلما كان عدد فترات التجزئة (أكثر، أقل) تكون مساحة المستطيلات الناتجة قريبة من المساحة الحقيقية المطلوبة.

كلمة أخيرة:

عندما نستخدم مجموع ريمان لتقدير المساحة بين منحنى اقتران ومحور السينات فإننا نراعي الأمور التالية، حتى نحصل على نتائج قريبة من الواقع:

- زيادة عدد فترات التجزئة.

- نحسب مجموع ريمان الناتج عن توصيل نقاط فترات التجزئة اليسارية.

- نحسب مجموع ريمان الناتج عن توصيل نقاط فترات التجزئة اليمينية.

- نأخذ متوسط المجموعين السابقين أو نحسب مجموع ريمان الناتج عن توصيل نقاط منتصف فترات التجزئة.

اكتبوا لنا ملاحظاتكم واستفساراتكم
تحرير: المدرسة العربية www.schoolarabia.net	إعداد: أ. فائق الفّرا / أ. سليم حمام
	تاريخ التحديث: آب 2002
	تاريخ التحديث: تموز 2012