|
||||||||||||||||||||||||||||
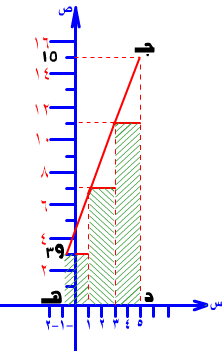
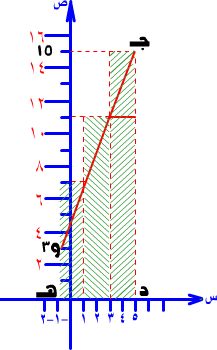
منحنى هذا الاقتران ومحور السينات باستخدام تجزئة ثلاثية منتظمة للفترة المعطاة، أي إيجاد مجموع ق (س) في الفترة والتجزئة المعطاة وسنعبر عن ذلك بالرمز م ( 3 s ، ق ). ملحوظة: سنقتصر في الأمثلة والتمارين على الاقترانات كثيرة الحدود.
المطلوب: أ) إبجاد المساحة بالتوصيل بين النقاط اليسارية (نقاط بداية الفترة الجزئية).
|
||||||||||||||||||||||||||||
|
Copyright © 2001 - 2012 SchoolArabia. All rights reserved الحقوق القانونية و حقوق الملكية الفكرية محفوظة للمدرسة العربية |
||||||||||||||||||||||||||||