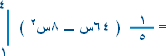تطبيقات على التكامل

Z المساحة المطلوبة = م₁ + م₂


= 24 وحدة مساحة .

التحقق من الحل :

من الشكل المنطقة المطلوب إيجاد مساحته هو مثلث

مساحته = مساحة شبه المنحرف ـ مجموع مساحة المثلثين .


× 20 × 5 ـ ( 8 + 18 )

= 50 ـ 26 = 24 وحدة مساحة ... وهذا هو نفس الجواب الذي حصلنا عليه من التكامل .

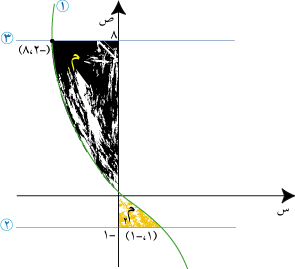
مثال 2 : جد مساحة المنطقة المحصورة بين المنحنى الذي معادلته ( ص + س³ = صفر ) ومحور الصادات والمستقيمات ص = -1 ، ص = 8 .

الحل :

ص + س³ = صفر

ق(س) = ص = ـ س³ ......................(1)

اقتران تكعيبي يمر بنقطة الأصل شكله

ص = -1 .....................................(2)

ص = 8 ......................................(3)

نقط التقاطع بين (1) ، (2)

هي عندما -1 = ـ س³

س = 1 Z أي ( 1 ، -1)

ونقط التقاطع بين (1) ، (3)

هي عندما 8 = ـ س³

س = -2 Z أي ( -2 ، 8)

م ( المساحة المطلوبة ) = م₁ + م₂

اكتبوا لنا ملاحظاتكم واستفساراتكم
تحرير: المدرسة العربية www.schoolarabia.net	إعداد: أ. فائق الفّرا
	تاريخ التحديث: آب 2004