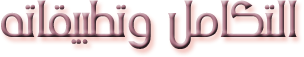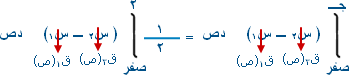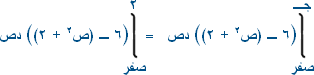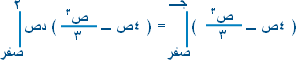الحل

بالتربيع

ص² = ( س ـ 2)   هذه معادلة قطع مكافئ سيني موجب رأسه ( 2 ، صفر ) والمنحنى بذلك يمثل الجزء الواقع فوق محور السينات منه لأن 

ص = +

ص=

س = 6  ............................. (2)

حسب المعطيات م₁ = م₂

 

بالتربيع ص² = س ـ 2

           س = ص² + 2

      ق(ص) = ص² + 2

     ق₂(ص) = س =   6

12جـ ـ جـ³ = 24 ـ 8

12جـ ـ جـ³ = 16

جـ³ ـ 12جـ + 16 = صفر

\ قيمة جـ تحقق هذه المعادلة .