|
التفكير ... |
 |
ق
(جـ)
= 3
ق (جـ) - 3 = صفر
ق (س) – 3 = صفر
س2 – 3س + 1 – 3 = صفر
س2 – 3س – 2 = صفر |
|
ق (س)
متصلاً في
[ -1 ، 2 ]
... كثير حدود
|
ق
(2) = 4 – 6 + 1 |
، |
ق
(-1) = 1 + 3 + 1 |
|
=
-1 |
، |
=
5 |
|
 |
|
 |
ـ
ق ( -1 )
¹
ق ( 2 ) وهما قيمتان مختلفتان في الإشارة.
3
تقع
بين
-1
،
5
أي
-1 < 3 < 5.
\
حسب النظرية
يوجد
قيمة واحدة على الأقل
جـ
'
(ه-1
، 2 )
بحيث
ق (جـ) = 3.
|
لإيجاد (
جـ
) :
نفرض
هـ (س)
= س2 – 3س – 2 ، س
'
[ه-1
، 2 ]
حيث :
هـ (س)
متصلاً في
[ -1 ، 2 ]
... كثير حدود.
هـ ( -1 ) = 1 + 3 – 2 ، هـ ( 2 ) = 4 – 6 – 2
\
هـ (س)
يحقق شروط نظرية بلزانو.
ـ
يوجد
قيمة
واحدة على الأقل
جـ
'
(ه-1
، 2 )
بحيث
هـ (جـ) = صفر
التي تعني بدورها أن
ق (س) = 3.
التقريب
الأول :
هـ (س)
= س2 - 3س - 2 = صفر
نجد قيمة
(س)
التقريبية من قانون المعادلة التربيعية ذات المجهول الواحد، حيث:
والجواب |
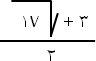 |
يهمل لأنه خارج المجال [ ـ 1 ، 2 ]. |
إذن |
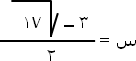 |
لأنها ضمن المجال [ ـ 1 ، 2 ]. |
| |
|
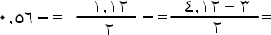 |
| |
|
ق ( -0.56)
@
3 |
أي أن
جـ = -0.56.
(مقربة لمنزلتين عشريتين)،
ويمكن أن نقدر قيمة
(جـ)
المطلوبة
بطريقة أخرى هي:
س2 - 3س - 2 = صفر
¬
س
(س-3) = 2
والعاملان
س (س - 3)
حاصل ضربهما موجب، فهما إما موجبان أو سالبان، فإذا كانا
موجبين يهملان لأنهما خارج نظاق المجال [ -1 ، 2 ] (لماذا؟)
وإما أن يكونا
سالبين فهما ضمن المجال وحيث تكون
س
(جـ)
المطلوبة أكبر من -1 وفي هذه الحالة يمكن أن نلجأ إلى عمليات
تقريب على الشكل التالي:
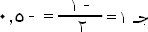 |
هـ (س)
سالب. |
| |
|
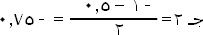 |
هـ (س)
سالب. |
| |
|
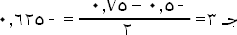 |
هـ (س)
سالب. |
| |
|
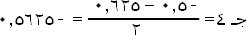 |
= -0.56 هـ
(س) = صفر (تقريباً) |
أي أن
جـ = - 0.56
هي التي تجعل
قيمة الاقتران
ق = 3
وهي واقعة في المجال
( -1 ، 2 ).....
وهو المطلوب.
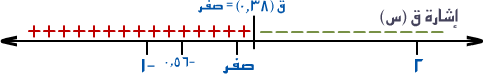 |
|
ق (-0.56) = 3 |
|