الشكل الرباعي
الدائري والزاوية الخارجة عنه
تعريف:-
إذا مدّ أحد
أضلاع الشكل الرباعي على استقامته، نسمي الزاوية المحصورة بين امتداد هذا الضلع
والضلع المجاور له، الزاوية الخارجة عن الشكل الرباعي .
نظرية :-
قياس الزاوية
الخارجة عن الشكل الرباعي الدائري يساوي قياس الزاوية المقابلة للمجاورة لها .
 |
المعطيات :-
أ ب جـ
د شكل رباعي دائري مدّ
 على
استقامته إلى هـ ( كما في الشكل ) على
استقامته إلى هـ ( كما في الشكل )
المطلوب :-
اثبات
أن قياس 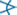 د
جـ هـ = قياس د
جـ هـ = قياس 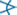 ب
أ د . ب
أ د . |
البرهان : -
بما أن أ ب جـ
د رباعي دائري فإن قياس 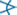 1 +
1 + 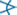 3
= 180 ْ
3
= 180 ْ
كذلك قياس 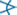 2
+ قياس
2
+ قياس 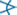 3
=180 ْ لأنهما متجاورتان على المستقيم ب جـ هـ .
3
=180 ْ لأنهما متجاورتان على المستقيم ب جـ هـ .
أي أن قياس 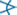 2 + قياس
2 + قياس 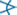 3
= قياس
3
= قياس 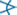 1+ قياس
1+ قياس 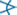 3
3
إذا قياس 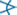 2
= قياس
2
= قياس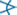 1
1
أي أن قياس
الزاوية الخارجة عن الشكل الرباعي = قياس الزاوية الداخلة فيه والمقابلة
لمجاورتها .
|
 |
مثال (3) :-
في
الشكل دائرتان متقاطعتان قي س ، ص قياس 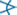 د جـ ص = 80 ْ
د جـ ص = 80 ْ
جد قياس
كل من:
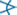 أ س ص ،
أ س ص ،
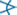 أ
ب ص. أ
ب ص.
الحل: |
تدريبات :
1)
أ ب ج د شكل رباعي
مرسوم داخل دائرة، مد ضلعه ب ج على استقامته من جهة ج ثم نصفت الزاوية الخارجة
الحادثة بمستقيم لا في محيط
الدائرة في هـ ، برهن على أن الوتر أ هـ ينصف الزاوية ب أ د .
|
 |
2)
تقاطعت دائرتان في أ، ب ثم رسم الوتران أص ، د ب في إحدى الدائرتين
ومدا على استقامتهما ليلاقيا الدائرة الأخرى في س ، جـ ( كما في الشكل
المجاور) .
برهن على أن جـ س¤¤ د
ص . برهن على كل حالة لوحدها. |
|
 |





