مثال 5 :
ليكن ق (س) , هـ (س) اقترانين متصلين في [ ـ2 , 7 ]
، وقابلين للإشتقاق في ( ـ2 , 7 ) بحيث:
ق( ـ2 ) = 1 , ق( 7 ) = 15
،
هـ ( ـ2 ) = ـ3 ,
هـ ( 7 ) = 11
|
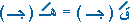 |
أثبت أنه يوجد قيمة واحدة على الأقل جـ
'
ه(
ـ2 , 7 ) بحيث
|
الحل :
|
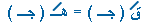 |
التفكير .... لكي نثبت أن : |
|
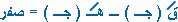 |
أي أن :
|
لذا نفترض
ل (س) = ق (س) ـ هـ (س) , س
'
ه[ ـ2 , 7 ] نحاول تطبيق شروط ( ن ـ رول ) على
ل (س).
الاتصال
:
ل (س) متصل في [ ـ2 ، 7 ] ؛ لأنه يتكون من الفرق بين اقترانين متصلين .
اáÇشتقاق
:
ل (س) متصل في ( ـ2 ، 7 ) ؛ لأنه يتكون من الفرق بين اقترانين قابلين للاشتقاق
حيث :
المساواة
:
ل ( ـ2 )
= ق ( ـ2 ) ـ هـ ( ـ2 )
ل ( ـ2 )
= 1 ـ ( ـ3 ) = 4
ل ( 7 ) =
ق ( 7 ) ـ هـ ( 7 )
ل ( 7 ) =
15 ـ 11 = 4
\
ل
( ـ2 ) = ل ( 7 ).
\
ل (س)
يحقق شروط نظرية رول.
\
يوجد قيمة واحدة على الأقل
جـ
'
( -2 ،
7 )
بحيث :
|

