|
-
ملاحظات على الطريقتين السابقتين :
1.
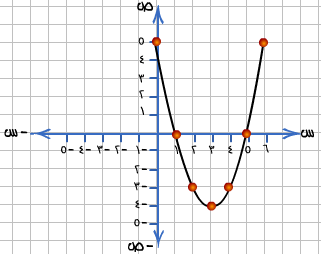
إذا كانت قيم المجهول في المعادلة التربيعية قيماً كسرية
أو أعداداً غير نسبية فلن تظهر في الجدول ولكنها ستظهر
بشكل تقريبي على منحنى القطع المكافئ، لذلك عند الرسم يجب
مراعاة الدقة كما يفضل استخدام الحاسوب في رسم المنحنى .
|
 |
أمثلة : |
|
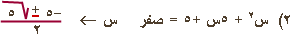 |
|
|
3)
س2 – 8.2 س +16 = صفر
س ¬ 3.2
، 5 . |
|
2. إذا
كانت قيم المجهول كبيرة مثلاً في معادلات مثل :
س2
 23 س
23 س
 570 = صفر حيث س = 38 و
570 = صفر حيث س = 38 و
 15
فيجب
مراعاة الأمر عند الرسم واستخدام مقياس مناسب حيث 1سم على
ورقة المربعات يمكن أن يمثل 5 أو عشر وحدات .....إلخ.
15
فيجب
مراعاة الأمر عند الرسم واستخدام مقياس مناسب حيث 1سم على
ورقة المربعات يمكن أن يمثل 5 أو عشر وحدات .....إلخ.
إن عمل
جدول بقيم س ، ق ( س ) في مثل هذه الحالات يتطلب بعض الوقت
.
يفضل
استخدام الطريقتين السابقتين حينما تكون قيم المجاهيل
صغيرة مثلاً
 10
³
س ³
+10 . 10
³
س ³
+10 .
3. نعود
ونؤكد عند استخدام هاتين الطريقتين ( وهما في الواقع طريقة
واحدة حيث أن ارتباط الواحدة بالأخرى يكون عضوياً ) على
ضرورة الرسم بمنتهى الدقة والأفضل أن يكون رسم المنحنى
باستخدام الحاسوب إذا كان الدارس قادراً على ذلك .
|