
أمثلة :
مثال 1) :
س ص ع مثلث قائم
الزاوية في ص ، فيه س ص = 5سم ، ص ع = 12سم
أوجد كلا من :
1) س ع ، 2) جا ع ، 3) جا س .
الحل
|
 |
مثال 2):
في لحظة
ما كانت المسافة بين قمة شجرة ورأس ظلها على سطح الارض تساوي 15م، وكان
جاس = 0.6، جد ارتفاع الشجرة (مستعيناً بالشكل المجاور ) .
الحل |
مثال3) :
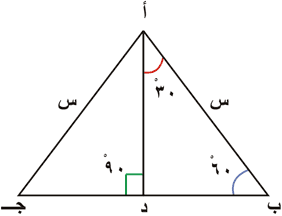 |
يمثل الشكل المجاور
مثلثاً متساوي الأضلاع، طول ضلعه س، أ د عمودي على الضلع ب ﺠ.
 |
اثبت أن
جا 30 = |
|
|
:
|
 |
2- |
|
 |
هي النسبة
المثلثية الأساسية الثانية وهي عبارة عن النسبة الناتجة عن قسمة طول الضلع
المجاور للزاوية على طول وتر المثلث.في
الشكل المجاور لقد رمزنا للزاوية القريبة من الرأس جـ بالرمز س ، والضلع
المجاور لها هو الضلع ب جـ
أما الوتر فهو أجـ ، إذن جيب تمام
|
تدريب :
ارجع إلى
المثلثات التي رسمتها في موضوع جيب الزاوية، أوجد جيب تمام الزاوية 50 ْ في كل
منها .
إذا كانت
قياساتك صحيحة ستجد أن جيب تمام الزاوية 50 ْ= 0.60-0.64 تقريباً.
|
) . |
 |
يرمز
لجيب تمام الزاوية بالرمز جتا أو
( |
السابق
الصفحة الرئيسية
التالي