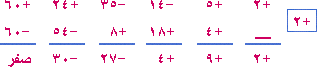تحليل كثيرات الحدود من الدرجة الثالثة فأكثر إلى عواملها الأولية

 

 

إجابة التدريب (1) :

4. 5س⁴ + 24س – 14س³ – 35س² + 2س⁵ + 60

التحليل :

- نلاحظ أن حدود المقدار غير مرتبة تنازلياً لذلك علينا أن نرتبها أولاً .

المقدار = 5س⁴ + 24س – 14س³ – 35س² + 2س⁵ + 60

- إذا دققت النظر في القدار تجد أنه يمكن تجزئته إلى ثلاثة أقواس كما يلي :

       = (2س⁵ + 5س⁴) – (14س³ + 35س²) + (24س + 60)

       = س⁴ (2س + 5) – 7س² (2س + 5) +12 (2س + 5)

والعامل المشترك فيها هو (2س + 5)

المقدار = (2س + 5) (س⁴ – 7س² + 12)

والعبارة س⁴ – 7س² + 12 هي عبارة تربيعية قابلة للتحليل

المقدار = (2س + 5) (س² – 4) (س² – 3)

        = (2س + 5) (س – 2) (س + 2) (س2 – 3)

 

طريقة ثانية :

نبحث عن العامل المشترك حسب نظرية الباقي مستخدمين عوامل الحد المطلق (60) وهي كثيرة :

   ق (س) = 2س⁵ + 5س⁴ – 14س³ – 35س² + 24س + 60

لو وجدنا ق (1) = 42              إذن س – 1 ليس عاملاً من عوامل المقدار

          ق (-1) = (18)         إذن س + 1 ليس عاملاً من عوامل المقدار

لنجرب  ق (2) = 2 (2)⁵ + 5 (2)⁴ – 14 (2)³ – 35 (2)² + 24 (2) + 60

                  = 2 ² (2 ⁴ + 5 (2)² – 14 (2) – 35 + 12 + 15)

                  = 4 (16 + 20 – 28 – 35 + 27)

                  = 4 (63 – 63)

                  = صفر           

إذن س – 2 هو أحد عوامل المقدار

نقسم المقدار 2س⁵ + 5س⁴ – 14س³ – 35س² + 24س + 60 على س – 2 قسمة تركيبية .

 

 

ناتج القسمة = 2س⁴ + 9س³ + 4س² – 27س – 30

ونتابع العمل بنظرية الباقي والقسمة التركيبية أو نجزِّيء المقدار الناتج عن القسمة إلى

(2س⁴ + 4س² – 30) + (9س³ – 27س) لنصل إلى النتيجة النهائية للتحليل وهي

(س – 2) (س + 2) (2س + 5) (س² – 3)

 

5. إجابة السؤال هي :

6س⁴ – 9س³ – 51س² – 36س

                  = 3س (2س³ – 3س² – 17س – 12)

                  = 3س (س – 4) (س + 1) (2س + 3)

وعليك أن تفتش عن طرق الحل بنفسك .

 

رجوع