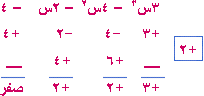تحليل كثيرات الحدود من الدرجة الثالثة فأكثر إلى عواملها الأولية

 

 

إجابة التدريب (1) :

3. 3س³ – 4س² – 2س – 4

التحليل : من الصعب تجزئة هذا المقدار ولكن تجزئته ممكنة ، جرّب أن تجزأه بنفسك .

 فإذا فرضنا أن المقدار = ق (س)

يكون ق (س) = 3س³ – 4س² – 2س – 4

ويكون ق (2) = 3 (2)³ – 4 (2)² – 2 (2) – 4

                = 24 – 16 – 4 – 4

                = 24 – 24

                = صفر

إذن س – 2 هو أحد عوامل المقدار المراد تحليله .

لنجد بالقسمة التركيبية ناتج قسمة المقدار على س – 2

 

إذن ناتج القسمة = 3س² + 2س + 2

وهي عبارة تربيعية غير قابلة للتحليل

إذن الناتج النهائي = 3س³ – 4س² – 2س – 4

                   = (س – 2) (3س² + 2س + 2)

 

ملاحظة : يمكن تجزئة المقدار كما يلي ولكن الوصول إلى هذه التجزئة ليس بالأمر السهل .

3س³ – 4س² – 2س – 4 = 3س³ – 6س² + 2س² + 2س – 4س – 4

والآن نجمع الحدود كل اثنين معاً كما يلي :

                               = (3س³ – 6س²) + (2س² – 4س) + (2س – 4)

                               = 3س² (س – 2) + 2س (س – 2) + 2 (س – 2)

والعامل المشترك فيها هو س – 2

إذن 3س³ – 4س² – 2س – 4 = (س – 2) (3س² + 2س + 2)