|
|||||||||||||||||||||||||||||
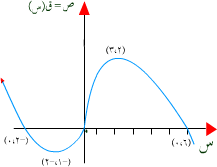
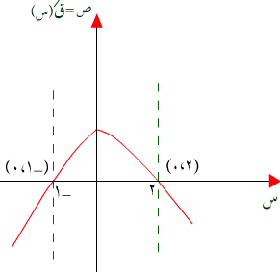
الحل :أولاً : فترات تزايد ق (س) هي ( ـ1 ، 2) .... حيث منحنى ق (س) صاعداًفترات تناقص ق(س) هي (ـ µ ، ـ1) ، (2 ، µ ) حيث منحنى ق(س) نازلاً (هابطاً)ثانياً : القيم القصوى
|
|||||||||||||||||||||||||||||
|
|
توضيح :عند س = ـ 1 ، 2
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
تحرير : المدرسة العربية www.schoolarabia.net |
اعداد : أ . فائق الفرا |
|
تاريخ التحديث : حزيران 2002 |
|
Copyright © 2001-2010 SchoolArabia. All rights reserved الحقوق القانونية و حقوق الملكية الفكرية محفوظة للمدرسة العربية