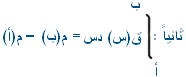الاقتران البدائي

نظرية :

نبحث في العلاقة بين التفاضل والتكامل

إذا كان ق(س) اقتراناً متصلاً في [ أ ، ب ] وعرف الاقتران المكامل له .

والاقتران البدائي له م(س) ، فإن :

أولاً : م(س) = جـ + ت(س) ( حيث جـ ثابت )

الاثبات :

حسب تعريف الاقتران المكامل ت(س) للاقتران ق(س)

ق(س) ............ (1)

وحسب تعريف الاقتران البدائي م(س) للاقتران ق(س)

ق(س) ............ (2)

من (1) ، (2)


	ـ

م(س) - ت(س) = جـ ( ثابت )

م(س) = جـ + ت(س)

بوضع س = أ

م(أ) = جـ + صفر

وتصبح المعادلة (3) هي :

................ (4) هـ.ط.ث أولاً

ومن المعادلة ( القاعدة (4) ) بوضع س = ب ينتج أن :


................ (5) هـ.ط.ث ثانياً		ـ

اكتبوا لنا ملاحظاتكم واستفساراتكم
تحرير: المدرسة العربية www.schoolarabia.net	إعداد: أ. فائق الفّرا
	تاريخ التحديث: آب 2004