حل نظام مكون من معادلتين تربيعيتين

أنظمة المعادلات وحلها

- حل نظام مكون من معادلتين تربيعيتين

مثال (3): قطعة أرض على شكل مثلث متساوي الساقين طول ساقه 50م ، ومساحة الأرض 1200م² ، أوجد طول قاعدتها وطول ارتفاعها .

الحل(3) : قبل كل شيء علينا أن نعمل رسماً تقريبياً للقطعة لأن الرسم يوضح أموراً كثيرة قد نغفل عنها إذا لم نرسم .

- نفرض أن ارتفاع قطعة الأرض ع م .

- وأن طول قاعدتها = 2 س م فيكون نصف طول قاعدتها = س م .

- ما نوع المثلث أ د ج من حيث الزوايا ؟

- إذا طبقنا نظرية فيثاغورس على المثلث أ د ج.

فإن

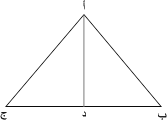
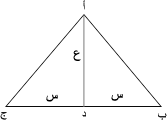
(50)² = ع² + س ² ............(1)

* ما القانون الذي نستخدمه لإيجاد مساحة مثلث ؟

* كم مساحة المثلث أ ب ج !

طول قاعدته × ارتفاعه

مساحة المثلث أ ب ج =

1200 = س × ع ..........(2)

الآن أصبح لدينا معادلتين س² + ع² = 2500 ........(1)

س ع = 1200 ........(2)

* يمكننا حل هاتين المعادلتين بعدة طرق كما عرفنا من الأمثلة السابقة ، وما علينا الآن إلا أن نختار واحدة منها .

* لنضرب المعادلة ...(1) في العدد 12 نحصل على د 12س² +12ع² = 2500×12

ولنضرب المعادلة ...(2) في العدد -25 فنحصل على -25 س ع = 1200 × (-25)

وبجمع المعادلتين الناتجتين نتخلص من الأعداد التي تشكل الطرف الأيسر للمعادلتين وينتج :

12 س² – 25 س ع + 12 ع² = صفر ……….(3)

ويمكننا الآن أن نحلل هذه المعادلة فنحصل على (4س -3ع) (3س - .........) = صفر أكمل الفراغ

........(4)		إذن 4 س – 3 ع = صفر ـ س =
........(5)		أو 3 س – 4 ع = صفر ـ س =

- يمكننا الآن أن نعوض قيمة س في إحدى المعادلتين للحصول على معادلة بمجهول واحد هو ع ، فإذا اخترنا المعادلة .......(2) نحصل على : س × ع = 00 12

× ع = 1200

3 ع ² = 1200×4

ع ² = 400×4

ع = ± 20×2

ع = ± 40

وبما أن ارتفاع الأرض لا يمكن أن يكون قيمة سالبة

إذن ارتفاع الأرض = 40 م .

أكمل بنفسك وأوجد طول القاعدة.

حل السؤال بطريقة أخرى .

انتبه فاللمسأله حلان بمعنى:-

ع = 40م ، أو ع = ........ م.

طول القاعدة ب ج = .......م أو ب ج =.........

حل السؤال بطريقة أخرى

اكتبوا لنا ملاحظاتكم واستفساراتكم
تحرير : المدرسة العربية www.schoolarabia.net	اعداد : المدرسة العربية
	تاريخ التحديث تشرين ثاني 2007