الزوايا والوضع القياسي لها ونسبها المثلثية

 

 

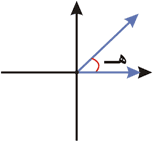
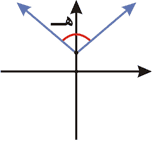
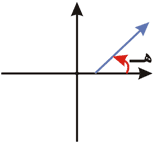
تمهيد:

 أي من الزوايا التالية في الوضع القياسي ؟

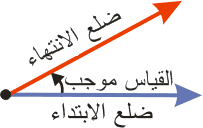
تعريف :

 تكون الزاوية في الوضع القياسي في المستوى الديكارتي، إذا كان رأسها نقطة الأصل، وضلع ابتدائها يقع على المحور الموجب السيني، وضلع انتهائها يقع في أحد الأرباع الأربعة أو على أحد المحاور.

 

تعلمت أن الزاوية هي زوج من الأشعة لهما نقطة البداية نفسها، وتسمى هذه النقطة رأس الزاوية، ويسمى أحد الشعاعين ضلع الابتداء للزاوية ويسمى الثاني ضلع الانتهاء.

 

ومما سبق يكون الشكل (ج) هوالذي يمثل الوضع القياسي للزاوية.

 

وقياس الزاوية هو عبارة عن مقدار دوران ضلع الابتداء حتى يأخذ وضع الانتهاء. ويكون القياس موجباً إذا دار ضلع الابتداء باتجاه يعاكس دوران عقارب الساعة، ويكون سالباً عندما يكون الدوران مع عقارب الساعة  كما في الشكلين.

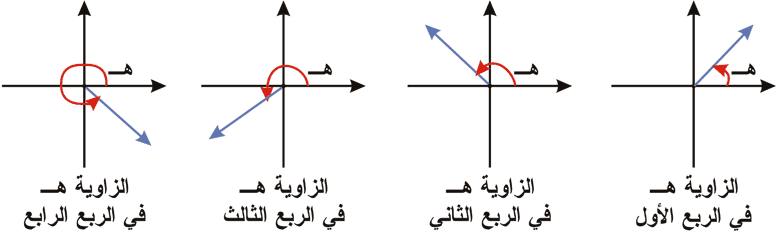
ومن تعريف الوضع القياسي للزاوية في المستوى الديكارتي

نقول أن الزاوية ﻫ تقع في الربع الأول إذا كانت  صفر ْ  < ﻫ ْ < 90 ْ

 

 

 

مثال-1-:-

 اذكر في أي ربع أوعلى أي محور يقع ضلع انتهاء كل من الزوايا التالية في وضعها القياسي.

أ‌) هـ =  120 ْ ،    ب) هـ = 60 ْ،   ج)هـ = 225 ْ ،    د )هـ = 90 ْ .                                          الحل:- 

 ثم ارسم كل منها في الوضع القياسي ؟                                                                         

ولكن متى تعتبر قيمة الزاوية سالبة ؟ إن الأمر يعتمد على دوران ضلع الابتداء فإذا كان دوران

ضلع الابتداء متوافقاً مع اتجاه دوران عقارب الساعة كانت الزاوية سالبة وهذا ما ذكرناه سابقاً .

 

مثال-2-:-

مثل كل من الزوايا التالية في الوضع القياسى لها على المستوى الديكارتي .

أ‌)  -60 ْ                              ب) -150                                 ج) -300 ْ.                            الحل:- 

ولكن الآن هل لاحظت أن ضلع انتهاء الزاوية (60 ْ) بالقياس الموجب هو نفس ضلع انتهاء الزاوية (300) بالقياس السالب؟     أي الزاوية 60 ْ = -300 ْ.

إن ما نريد أن نتوصل إليه هو أنه يمكن أن تشترك عدة زوايا في ضلع الانتهاء في الوضع القياسي.

فالزوايا جميعها التي على الصورة (ﻫ + ن × 360 ْ ) حيث ن عدد صحيح، لها ضلع الانتهاء نفسه . وبمعنى آخر أن ضلع انتهاء الزاوية ﻫ في الوضع القياسي هو نفسه ضلع انتهاء الزاوية ( ﻫ + ن × 360 ْ ) في الوضع القياسي. ولتوضيح هذا المفهوم نأخذ المثال التالي:-

 

مثال-3-:-

في أي ربع أو على أي محور يقع ضلع الانتهاء لكل من الزوايا التالية في الوضع القياسي لها ؟

أ‌)  -150 ْ ،    ب) 410 ْ   ،   ج) 720 ْ .                                                                               الحل:- 

وبعد هذا المثال وباختصار نقول إذا كانت الزاوية بالقياس السالب نجمعها مع 360 ْ أو مضاعفاتها، اما إذا كانت الزاوية بالقياس الموجب وأكبر من 360 ْ، فنطرح منها360 ْ أو مضاعفاتها.

مثال-4-:-

 حدد في أي ربع أو على أي محور يقع ضلع الانتهاء لكل من الزوايا التالية في الوضع القياسي.

أ‌)    240 ْ ،    ب) -90 ْ،   ج) 180 ْ ،    د ) 540 ْ ،      د ) 200 ْ .                                        الحل:- 

 

الصفحة الرئيسية