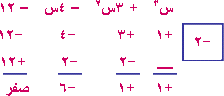علم الجبر

مراجعة عامة في تحليل المقادير الجبرية إلى عواملها الأولية

7- المقدار هو عبارة عن كثير حدود ، ويوجد أكثر من طريقة لتحليله .

الطريقة الأولى :

نبحث عن قيم س التي تجعل قيمة المقدار = صفر

فنجد أن س = 1 ، س = -2

فإذا فرضنا أن ق(س) = س⁴ + 2س³ – 7س² – 8س + 12

إذن ق(1) = (1)⁴ + 2(1)³ – 7(1)² – 8 (1) + 12

= 1 + 2 – 7 – 8 + 12

= 15 – 15

= صفر

إذن س – 1 هو أحد عوامل المقدار

بطريقة مشابهة نجد أن ق(-2) = صفر

وأن س + 2 هو عامل آخر من عوامل المقدار

- كيف يمكن أن نعرف بقية العوامل ؟

نقسم المقدار على س – 1 قسمة تركيبية .

إذن ناتج القسمة = س³ + 3س² – 4س – 12

نقسم ناتج القسمة تركيبياً أيضاً على س + 2

ناتج القسمة = س² + س – 6

وهو عبارة تربيعية قابلة للتحليل

س² + س – 6 = (س + 3) (س – 2)

إذن س⁴ + 2س³ – 7س² – 8س + 12

= (س – 1) (س + 2) (س + 3) (س – 2)

الطريقة الثانية :

يمكن أن نجزِّأ المقدار المعطى كما يلي :

(س⁴ + 2س³) – (7س² + 8س – 12)

= س³ (س + 2) – (7س – 6) (س + 2)

= (س + 2) (س³ – 7س + 6) لأن (س + 2) عامل مشترك

يمكن الآن أن نجزِّأ المقدار الجديد كما يلي :

= (س³ – س) – (6س – 6)

= س (س² – 1) – 6 (س – 1)

= س (س – 1) (س + 1) -6 (س – 1)

= (س – 1) (س (س + 1) -6)

= (س – 1) (س² + س – 6)

نحلل س² + س – 6 فهي عبارة تربيعية بسيطة

س² + س – 6 = (س + 3) (س – 2)

إذن الناتج النهائي

س⁴ + 2س³ – 7س² – 8س + 12

= (س + 2) (س – 1) (س + 3) (س – 2)

اكتبوا لنا ملاحظاتكم واستفساراتكم
تحرير : المدرسة العربية www.schoolarabia.net	اعداد : أ. سليم حمام
	تاريخ التحديث تموز 2002
	تاريخ التحديث كانون الأول 2008