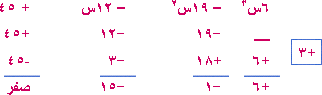تحليل كثيرات الحدود من الدرجة الثالثة فأكثر إلى عواملها الأولية

 

 

إجابة التدريب (2) :

 

1. 4س³ + 9س² – 8س + 3 = (س + 3) (4س² – 3س + 1)

 

2. 6س⁴ – 7س³ – 10س² + 17س – 6 = (س – 1)² (2س + 3) (3س – 2)

 

3. 3س³ – 12س + س⁴ – 8 -2س² = س⁴ + 3س³ – 2س² -12س – 8

= (س + 2)² (س – 2) (س + 1)

 

4. س² – 48س³ + 8س⁵ + 8س⁴ – 6 + س = 8س⁵ + 8س⁴ – 48س³ + س² + س – 6

= (8س⁵ + 8س⁴ – 48س³) + (س² + س – 6)

= 8س³ (س² + س – 6) + (س² + س – 6)

وبأخذ العامل المشترك (س² + س – 6)

= (س² + س – 6) (8س³ + 1)

= (س + 3) (س – 2) (2س + 1) (4س² – 2س + 1)

جرّب الحل بنظرية الباقي والقسمة التركيبية بنفسك .

 

5. 6س³ – 19 س² – 12س + 45

الحل : نطبق نظرية الباقي على أحد عوامل العدد (45)

ولنأخذ س = 3

6س³ – 19س² – 12س + 45 = 6 (3)³ – 19 (3)² – 12 (3) + 5 (3)²

                                      = 3 ² (18 – 19 – 4 + 5)

                                     = 3 × 3 (23 – 23)

                                     = صفر

إذن س – 3 هو أحد عوامل المقدار

نجري الآن عملية قسمة تركيبية

 

الناتج 6س² – س – 15

والناتج عبارة تربيعية قابلة للتحليل حيث

6س² – س – 15 = (2س + 3) (3س – 5)

إذن الناتج النهائي = (س – 3) (2س + 3) (3س – 5)

 

6. س⁴ + 4

الحل : لا يوجد قيمة = صفر للاقتران ق (س) = س⁴ + 4

لأن س⁴ هي صفر أو عدد موجب . وعلى ذلك فلا يمكن تحليل هذا المقدار بنظرية الباقي والقسمة التركيبية.

ما هو الحل إذن لا شك أنك تذكر طريقة إكمال المربع .

س⁴ + 4س² + 4 – 4س²       إضافة وطرح 4س²

(س⁴ + 4س² + 4)  -4س²

(س² + 2)² – 4س² = (س² + 2 – 2س) (س² + 2س + 2س)

 

رجوع