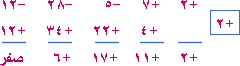تحليل كثيرات الحدود من الدرجة الثالثة فأكثر إلى عواملها الأولية

 

مثال (4) :

حلل المقدار س⁴ – 13س² + 36 + 72س – 26س³ + 2س⁵ .

 

الحل :

- نرتب المقدار حسب قوى (س) التنازلية :

2س⁵ + س⁴ – 26س³ – 13س² + 72س + 36

- عوامل العدد 36 هي ± 1 ، ± 2 ، ± 3 ، ± 4 ، ± 6 ،  ± 12 ، ... الخ .

- لناخذ العامل س – 1 حيث س = 1

ونفرض ق (س) = 2س⁵ + س⁴ – 26س³ – 13س² + 72س + 36

          ق (1) = 2(1)⁵ + (1)⁴ – 26 (1)³ – 13 (1)² + 72 (1) + 36

                   = 2 + 1 – 26 – 13 + 72 + 36

                   = 111 – 39

                   = 72

إذن س – 1 ليست من العوامل ، ولو جربنا س+ 1 لوجدناها أيضاً ليست من العوامل .

 

- دعنا نجرب ق (3) = 2(3)⁵ + (3)⁴ – 26 (3)³ – 13 (3)² + 72 (3) + 36

                      = 3 (2 (3)⁴ + (3)³ – 26 (3)² – 13 (3) + 72 + 12)

                      = 3 (162 + 27 – 234 – 39 + 72 + 12)

                      = 3 × 3 (54 + 9 – 78 – 13 + 24 + 4)

                      = 9 (63 – 91 + 28)

                      = 9 (91 – 91)

                      = 9 × صفر

                      = صفر 

إذن س – 3 هو أحد عوامل المقدار

- نقسم المقدار 2س⁵ + س⁴ – 26س³ – 13س² + 72س + 36 على س – 3

 

 

ناتج القسمة = 2س⁴ + 7س³ – 5س² – 28س – 12

- لنجرب على ناتج القسمة ق₁ (س) = 2س⁴ + 7س³ – 5س² – 28س – 12 عاملاً آخراً هو (2)

 ق₁ (2) = 2 (2)⁴ + 7 (2)³ – 5 (2)² – 28 (2) – 12

ق1 (2) = 32 + 56 – 20 – 56 – 12

          = 32 + 56 – 56 – 32

          = صفر

إذن س – 2 هو أحد عوامل ق₁

 

- لنقسم المقدار 2س⁴ + 7س³ – 5س² – 28س – 12 على س – 2 بالطريقة التركيبية .

 

ناتج القسمة = 2س³ + 11س² + 17س + 6

- ويمكن أن نستمر في نظرية الباقي وتجربة عامل جديد ... تابع الموضوع بنفسك .

- أو نجرب تجزئة المقدار 2س³ + 11س² + 17س + 6 فقد يصبح قابلاً للتحليل .

2س³ + 11س² + 17س + 6 = 2س³ + 11س² + 5س + 12س + 6

                                   = (2س³ + 11س² + 5س) + (12س + 6)

بإخراج العامل المشترك           = س (2س² + 11س + 5) + 6 (2س + 1)

بتحليل العبارة التربيعية            = س (2س + 1) (س + 5) + 6 (2س + 1)

أخذ العامل المشترك               = ( (2س + 1) (س (س + 5) + 6) )

                                   = ( (2س + 1) (س² + 5س + 6) )

بتحليل العبارة التربيعية           = (2س + 1) (س + 2) (س + 3)

إذن تحليل المقدار 2س⁵ + س⁴ – 26س³ – 13 س² + 72س + 36

                 = (س – 3) (س – 2) (2س + 1) (س + 2) (س + 3)

 

رجوع