نظرية
بور لذرة الهيدروجين
اعتمادا
على افكار بلانك واينشتاين ، استطاع العالم بور تفسير طيف
ذرة الهيدروجين وحساب طاقة الإلكترون فيها . وهذا
هو ملخص نظرية بور على شكل نقاط :
1-هنالك
مجموعة محددة من المدارات الدائرية (مستويات الطاقة) يدور
فيها الكترون ذرة الهيدروجين حول النواة ويمكن التعبير عنها
بالارقام 1 ، 2 ، 3
….إلخ من الأقرب إلى الأبعد عن النواة .
2-ما
دام الإلكترون يحتل نفس المدار ولا يغيره فإنه لا يشع ضوءا
(طاقة) ولا يمتصها.
3-يمكن للإلكترون أن ينتقل من مستوى إلى مستوى
آخر بحيث :
تشع
الذرة طاقة اذا انتقل الالكترون من مستوى ذو طاقة عالية إلى
مستوى ، ذو طاقة أخفض, وينتج عن هذا الانتقال
طيف الاشعاع الخطي الذي يمثل الفرق بين المستويين .

· تمتص
الذرة الطاقة بكميات محددة اذا انتقل الإلكترون من مستوى ذو
طاقة منخفضة إلى مستوى ذو طاقة أعلى أي عندما تهيج الذرة
باعطائها كمية من الطاقة من مصدر خارجي . أنظر الشكل

لقد
استطاع بور وضع معادلة رياضية حسب بواسطتها طاقة الالكترون
في كل مستوى من هذه المستويات . وهذه هي المعادلة وسنأخذها
مسلما بها :


بسبب
التجاذب بين الالكترون والنواة ، وهذا التجاذب يصبح صفرا عندما
يبتعد الالكترون كثيرا عن النواة إذن طاقة الالكترون
المتجاذب مع النواة تكون سالبة وتكون سالبة أكثر كلما كان
الإلكترون أقرب
إلى النواة . لاحظ أن المسافات بين مستويات الطاقة تصغر كلما
كبرت قيمة (n) وهذا يعني أن فرق الطاقة بين مستويين متاليين
يصبح صغيرا جدا .
يمكن
باستخدام معادلة بلانك ط = ثابت بلانك
× التردد
وبمعادلة
بور
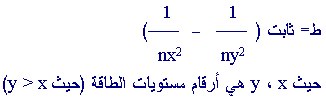
مثال : ما طول
موجة الضوء (مقاسة بالنانومتر) المنبعث عند اتنقال الإلكترون
في ذرة الهيدروجين من المستوى الخامس إلى المستوى الثاني ؟
تحليل
السؤال :
1)
ما المستوى الذي كان
فيه الالكترون في الاصل ؟
الجواب : المستوى ………………
2) إلى
أي مستوى انتقل الالكترون
؟
الجواب
: الى المستوى …………….
3) أيهما
اعلى في طاقته المستوى الخامس أم المستوى الثاني ؟
4) عند
انتقال الالكترون من المستوى الخامس ( ذو الطاقة العالية )
إلى المستوى الثاني ( ذو الطاقة المنخفض فإنه يصدر طاقة .
5) كيف نحسب
مقدار الطاقة التي يبعثها الالكترون ؟
يمكننا
ذلك باستخدام معادلة بلانك او معادلة بور .
6) من
معطيات السؤال يمكن استخدام معادلة بور لوجود الكميات الضرورية
، اما معادلة بلانك ففيها كميتان مجهولتان هما الطاقة والتردد
، ولذلك نبدأ بمعادلة بور .
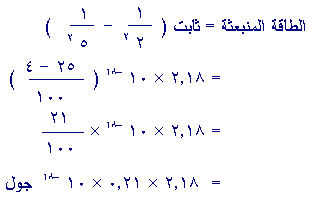
7)
قد عرفنا قيمة الطاقة المنبعثة ، ويمكننا الان ان نحسب التردد
من معادلة بلانك :
الطاقة
المنبعثة = ثابت بلانك × التردد
2.18 × 0.21 × 10 –18 =
63.06 × 10 34 × التردد
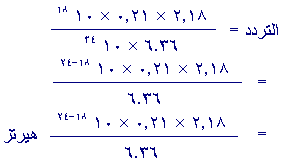
8)
نعلم من الفيزياء ان سرعة الضوء = 3 × 810 م/ث
9) ما العلاقة بين سرعة
الضوء وتردده وطول موجته ؟
السرعة
= التردد × طول الموجة
وهذه
العلاقة تقودنا إلى المطلوب في السؤال وهو طول الموجة

= 43.45
× 10 9-8 نانومتر
=
43.45 × 10 نانومتر
= 435.5 نانومتر
مسائل
للحل
1-
إذا علمت أن طاقة أحد المستويات في ذرة الهيدروجين
هو
–6.06 × 10-20
جول فما رقم هذا المستوى ؟
2-
إذا سقط الإلكترون في ذرة الهيدروجين من المستوى الخامس إلى
المستوى الرابع ، فاحسب :
أ.
تردد موجة الضوء المنبعث .
ب.طول
موجته .
ج-في
أي جزء من الطيف الكهرومغناطيسي يقع هذا الاشعاع
.
3. احسب الطاقة (بالجول)
التي يملكها مول واحد من الفوتونات التي لها طول موجي = 546
نانومتر .
4.يمكن
تطبيق نظرية بور على انواع اخرى غير الهيدروجين وتحوي الكترون
واحد ، مثل He+1 ، Li+2
،
Be+3 ، ….الخ
، وفي مثل هذه الحالات تكون طاقة المستوى n
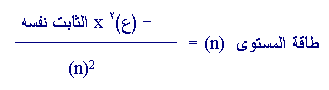
حيث
ع : هي العدد الذري للنوع المدروس .
المطلوب
منك :
1- ما
طاقة المستوى الاول (n=1) لايون الهيليوم He+1 ؟
2- ما
طاقة المستوى الثالث (i3=n) لايون الليثيوم Li+2 ؟
3- ما طاقة المستوى الخامس
(i5=n) لايون Be+3 ؟





