|
|
ضرب المتجه بعدد نسبي
Multiplication by a Rational No : |
|
قاعدة (1) :
إذا كان أ ، ب متجهان متوازيان فإن أ = ب جـ حيث
جـ عدد حقيقي
. |
إن هذا أمر بديهي لأنه ما دام المتجهان متوازيان فإنهما إما أن
يكونا متساويين وفي هذه الحالة جـ = 1 ، وإما أن يكونا غير
متساويين وفي هذه الحالة جـ أكبر من 1 ، أو جـ أصغر من 1 .
لاحظ الشكل الذي يضم مجموعة من المتجهات المتوازية هي :
|
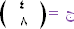 |
هـ =
( 3 ، 6 ) |
ي=
( 2 ، 4 ) |
|
و=
( 2 ، 4 ) |
|
|
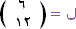 |
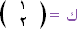 |
|
 |
|
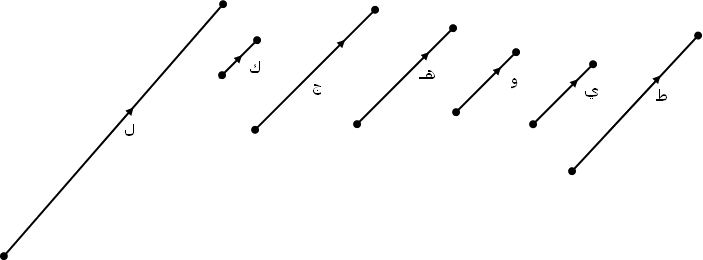 |
لاحظ أيضاً أن المتجهات المتوازية إما أن تكون متساوية مثلاً و
= ي ، أو أن يكون الواحد من مضاعفات الآخر .مثل ج = 2 و ، أو
جزءاً منه
|
قاعدة (2) :
إذا كان أ ، ب متجهان غير متوازيين وكان جـ أ = د
ب فإن جـ = د = صفر ، كيف تفسر هذا الأمر ؟ |
|
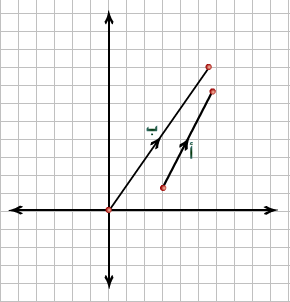 |
أ ، ب متجهان غير متوازيين إن جـ أ لا يمكن أن
يساوي د
ب
حيث جـ ، د عددان نسبيان غير الصفر ، لأن لهما
اتجاهين مختلفين
( بينهما زاوية ) ، وبكلام آخر لا يمكن أن يتساوى
متجهان بينهما زاوية ، فهما قد يتساويان في القيمة
المطلقة ولكن يبقى اتجاه كل واحد منهما مختلف عن
الآخر . |

|

